Física Computacional - Pêndulo Simples, Não-Amortecido, Não-Forçado e no Limite de Pequenas Oscilções
Física Computacional é um novo tópico do meu blog, pois foi o curso que mais gostei na faculdade de física, o que mais me envolveu e é o ramo da física que sonho em fazer uma carreira.
Sem delongas, resolvi começar a divulgar meus estudos sobre oscilações e como são tratadas computacionalmente.
É um tema fascinante e quero aqui compartilhar tudo que aprendi ao estudá-lo, começando do mais simples (MHS) e indo aos poucos até o mais complicado (CAOS).
Neste primeiro post, começarei com o pêndulo simples executando um MHS (Movimento Harmônico Simples). Vou mostrar agora como desenvolver a equação do pêndulo simples, não-amortecido, não forçado e no limite de pequenas oscilações.
Sem delongas, resolvi começar a divulgar meus estudos sobre oscilações e como são tratadas computacionalmente.
É um tema fascinante e quero aqui compartilhar tudo que aprendi ao estudá-lo, começando do mais simples (MHS) e indo aos poucos até o mais complicado (CAOS).
 |
| Pêndulo Simples |
Da figura acima, observa-se que a componente da força peso que é responsável pelo movimento oscilatório do pêndulo, é aquela que é perpendicular à força de tensão na corda do pêndulo.
 |
| Decomposição da força peso |
Assim, temos:
$$P_{\theta} = -m*g*sin(\theta)$$
Só que, para pequenas oscilções $sin(\theta) \approx \theta$, logo
$$P_{\theta} = -m*g*sin(\theta) = m*g*\theta$$
Como $P_{\theta} = m*l*\frac{d^2\theta}{dt^2}$, temos que:
$$\frac{d^2\theta}{dt^2} + \frac{g}{l}*\theta = 0$$
Ou seja, a equação do pêndulo simples é uma equação diferencial ordinária homogênea de segunda ordem. A solução analítica para essa questão é: $\theta(t)=\theta_0*cos(\Omega*t+\phi)$, mas o objetivo desta publicação é usar métodos numéricos para solucionar esta EDO.
Essa EDO de segunda ordem, também pode ser escrita como duas EDOs de primeira orderm:
Primeira: $\omega(t)=\frac{d\theta(t)}{dt}$
Segunda: $\frac{d\omega(t)}{dt}=-\frac{g}{l}*\theta(t)$
Os métodos escolhidos são:
1- Método de Euler
2- Método de Euler-Cromer
3- Método de Runge-Kutta
Esses métodos foram criados para solucionar EDOs, mas dependendo da EDO um método pode ser mais eficaz ou menos eficaz que outro. Aqui estarei explicando cada método, mostrarei os resultados e qual método é o mais eficaz para estudar o movimento oscilatório.
Em todas as aplicações abaixo, foram consideradas as seguintes condições iniciais e constantes:
$\theta_0 = 0.2 rad$
$\omega_0 = 0.0 rad/s$
$g = 9.8 m/s^2$
$l = 1 m$
$m = 1 Kg$
$\Delta t = 0.04 s$
1 - Aplicando o Método de Euler
Pelo método de Euler, temos que $\frac{d\omega}{dt} \approx \frac{\omega(t+\Delta t) - \omega(t)}{\Delta t}$. Contudo, também temos que $\frac{d\omega}{dt} = -\frac{g}{l}*\theta$, logo:
$$\omega(t+\Delta t) = \omega(t) - \frac{g}{l}*\theta(t)*\Delta t$$
Também temos que $\frac{d\theta}{dt} \approx \frac{\theta(t+\Delta t) - \theta(t)}{\Delta t}$. Contudo, também temos que $\frac{d\theta}{dt} = \omega$, logo:
$$\theta(t+\Delta t) = \theta(t) + \omega(t)*\Delta t$$
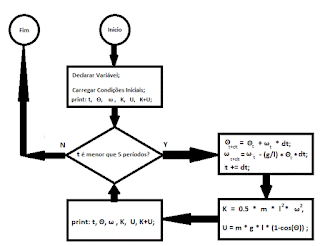
O algoritmo para o método de Euler ficou da seguinte forma:
Onde $K$ é a energia cinética do pêndulo e $U$ a energia potencial.
Fiz um programa em linguagem C para testar o método. Segue abaixo o código do programa.
/*
Programa: euler.c
Objetivo: Usar o método de Euler para resolver a equação diferencial
do Pêndulo Simples, Pêndulo não-amortecido, não-forçado, e
para pequenas oscilações
Autor: Alex Souza Marques
*/
#include <stdio.h>
#include <math.h>
#define MAX 250 // Número máximo de iterações
#define g 9.8 // Aceleração da gravidade
#define l 1 // Comprimento do pêndulo
#define dt 0.04 // Tamanho do passo
#define m 1 // Massa do pêndulo
int main(){
FILE *out;
float t=0, aux;
float w=0, o=0.2; // Omega e Theta
float K, U; // Energia Cinética e Energia Potencial
out=fopen("euler.dat","w"); // Arquivo para saída dos dados
K=0.5*m*l*l*w*w;
U=m*g*l*(1-cos(o));
fprintf(out,"%f\t%f\t%f\t%f\t%f\t%f\n",t,o,w,K,U,K+U); // Imprime as condicoes iniciais
/*Aplicando o método de Euler*/
for(t=dt;t<=5*2*M_PI*sqrt(l/g);t+=dt){ // Itera por 5 períodos do pêndulo
aux=w;
w=w-(g/l)*o*dt;
o=o+aux*dt;
K=0.5*m*l*l*w*w;
U=m*g*l*(1-cos(o));
fprintf(out,"%f\t%f\t%f\t%f\t%f\t%f\n",t,o,w,K,U,K+U); // Imprime o resultado
}
fclose(out);
return 0;
}
Este programa gera um arquivo com a saída dos resultados (euler.dat) para os 5 primeiros períodos do pêndulo.
Após rodar o programa, usei o software Gnuplot para visualizar os resultados. Segue abaixo um exemplo de script usado para carregar os dados no Gnuplot.
# Script: pendulo.gpl
# Objetivo: Imprimir os dados do programa runge_kutta.c
# Autor: Alex Souza Marques
reset;
set grid;
set xlabel "Tempo";
set ylabel "Ângulo";
set title "Método de Euler - Tempo x Ângulo";
#set key left;
#set yrange [0:0.27];
plot "euler.dat" u 1:2 title "Método de Euler - Tempo x Ângulo";
#rep "euler.dat" u 1:5 title "Método de Euler - Tempo x Energia Potencial" w l;
#rep "euler" u 1:6 title "Método de Euler - Tempo x Energia Total" w l;
Agora, segue os resultados encontrados usando o método de Euler:
Observe como a energia aumenta com o tempo, mostrando que o método de Euler não é eficiente para calcular movimentos oscilatórios. Após fazer outras simulações. diminuindo o tamanho do passo ($\Delta t$), foi observado que não há uma melhora apreciável.
Futuramente pretendo fazer um post sobre decaimento radioativo, onde o método de Euler mostra-se eficiente.
2 - Aplicando o Método de Euler-Cromer
Existe um valor $t_i$ dentro do intervalo $[t, t+\Delta t]$ correspondente a solução exata da derivada $\frac{d\theta}{dt}$. O problema do método de Euler é que ele toma $t_i$ no início do intervalo.
O método de Euler-Cromer, toma esse valor no final do intervalo. Abaixo, segue o algoritmo do método de Euler-Cromer. Note como a diferença é mínima em relação ao algoritmo anterior.
Escrevi o seguinte programa em linguagem C para aplicar o método:
/*
Programa: euler_cromer.c
Objetivo: Usar o método de Euler-Cromer para resolver a equação
diferencial do Pêndulo Simples, não-amortecido,
não-forçado e para pequenas oscilações
Autor: Alex Souza Marques
*/
#include <stdio.h>
#include <math.h>
#define g 9.8 // Aceleração da gravidade
#define l 1 // Comprimento do pêndulo
#define dt 0.04 // Tamanho do passo
#define m 1 // Massa do pêndulo
int main(){
FILE *out;
float t=0;
float w=0, o=0.2; // Omega e Theta
float K, U; // Energia Cinética e Energia Potencial
out=fopen("euler_cromer.dat","w"); // Arquivo para saída dos dados
K=0.5*m*l*l*w*w;
U=m*g*l*(1-cos(o));
fprintf(out,"%f\t%f\t%f\t%f\t%f\t%f\n",t,o,w,K,U,K+U); // Imprime as condicoes iniciais
/*Aplicando o método de Euler-Cromer*/
for(t=dt;t<=5*2*M_PI*sqrt(l/g);t+=dt){ // Itera por 5 períodos do pêndulo
w=w-(g/l)*o*dt;
o=o+w*dt;
K=0.5*m*l*l*w*w;
U=m*g*l*(1-cos(o));
fprintf(out,"%f\t%f\t%f\t%f\t%f\t%f\n",t,o,w,K,U,K+U); // Imprime o resultado
}
fclose(out);
return 0;
}
Esse programa gera o arquivo euler_cromer.dat, com a saída dos resultados. Usando o script do método anterior com pequenas alterações, foram obtidos os seguintes resultados.
Observem como a energia total do sistema oscila com este método. Contudo ela está oscilando sempre dentro de um mesmo valor médio e não cresce com o tempo. Se o tamanho do passo ($\Delta t$) for menor a melhora é significativa. Esse método se mostrou eficaz e preciso.
3 - Aplicando o Método de Runge-Kutta
Esse método consiste em usar o método de Euler para achar a função no centro do intervalo $[t, t+\Delta t]$, e depois usar o método Leap-Frog, que faz a derivada no centro do intervalo.
Abaixo segue o algoritmo para esse método.
Usando este algoritmo, escrevi o seguinte programa em Linguagem C:
/*
Programa: runge_kutta.c
Objetivo: Usar o método de Runge-Kutta para resolver a equação
diferencial do Pêndulo Simples, não-amortecido,
não-forçado e para pequenas oscilações
Autor: Alex Souza Marques
*/
#include <stdio.h>
#include <math.h>
#define g 9.8 // Aceleração da gravidade
#define l 1 // Comprimento do pêndulo
#define dt 0.04 // Tamanho do passo
#define m 1 // Massa do pêndulo
int main(){
FILE *out;
float t=0, aux, aux2, aux3;
float w=0, o=0.2; // Omega e Theta
float K, U; // Energia Cinética e Energia Potencial
out=fopen("runge_kutta.dat","w"); // Arquivo para saída dos dados
K=0.5*m*l*l*w*w;
U=m*g*l*(1-cos(o));
fprintf(out,"%f\t%f\t%f\t%f\t%f\t%f\n",t,o,w,K,U,K+U); // Imprime as condicoes iniciais
/*Aplicando o método de Runge-Kutta*/
for(t=dt;t<=5*2*M_PI*sqrt(l/g);t+=dt){ // Itera por 5 períodos do pêndulo
aux=w;
aux2=o;
w=w-(g/l)*o*dt/2; // Aplica Euler para achar o omega do meio
aux3=w;
o=o+aux*dt/2; // Aplica Euler para achar o theta do meio
w=aux-(g/l)*o*dt; // Acha o próximo omega
o=aux2+aux3*dt; // Acha o próximo theta
K=0.5*m*l*l*w*w;
U=m*g*l*(1-cos(o));
fprintf(out,"%f\t%f\t%f\t%f\t%f\t%f\n",t,o,w,K,U,K+U); // Imprime o resultado
}
fclose(out);
return 0;
}
Este programa cria o arquivo rung_kutta.dat, que contém a saída dos resultados. Usando o script do primeiro método com algumas poucas alterações, foram produzidos os seguintes resultados com o Gnuplot:
Observe que neste método a energia total do sistema oscila com uma amplitude muito menor para o mesmo tamanho de passo, se comparar com o método de Euler-Cromer. Contudo, a energia cresce com o tempo, mesmo que numa taxa bem mais baixa, se comparar com o método de Euler.
Conclusão
Dos três métodos que apresentei aqui, o que se mostrou mais estável para o estudo de oscilações foi o método de Euler-Cromer. Mesmo o método de Runge-Kutta sendo mais preciso, assim como no método de Euler, ele não conserva a energia do sistema.
No próximo post será apresentado meu estudo sobre o Pêndulo Simples, mas com amortecimento, aplicando Euler-Cromer.




















Comentários
Postar um comentário